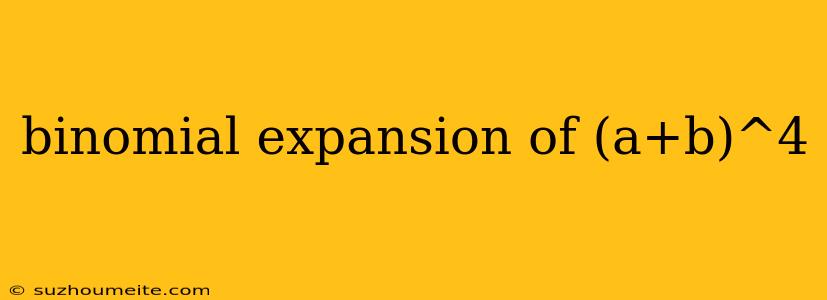Binomial Expansion of (a + b)^4
The binomial theorem provides a formula for expanding expressions of the form (a + b)^n, where 'n' is a positive integer. This theorem is very useful in algebra, calculus, and probability.
Understanding the Pattern
Let's explore the expansion of (a + b)^4:
- Start with the base case: (a + b)^1 = a + b
- Multiply by (a + b) for each increasing power:
- (a + b)^2 = (a + b)(a + b) = a^2 + 2ab + b^2
- (a + b)^3 = (a + b)(a^2 + 2ab + b^2) = a^3 + 3a^2b + 3ab^2 + b^3
- (a + b)^4 = (a + b)(a^3 + 3a^2b + 3ab^2 + b^3) = a^4 + 4a^3b + 6a^2b^2 + 4ab^3 + b^4
Notice the following patterns:
- Coefficients: The coefficients of the terms follow a pattern known as Pascal's Triangle.
- Exponents: The exponents of 'a' decrease from 4 to 0, while the exponents of 'b' increase from 0 to 4.
Using the Binomial Theorem
The binomial theorem provides a more concise way to expand (a + b)^4:
(a + b)^4 = ⁴C₀ a⁴b⁰ + ⁴C₁ a³b¹ + ⁴C₂ a²b² + ⁴C₃ a¹b³ + ⁴C₄ a⁰b⁴
where:
- ⁴Cₓ represents the binomial coefficient, calculated as ⁴Cₓ = 4! / (x! * (4-x)!)
- x ranges from 0 to 4
Calculating the binomial coefficients:
- ⁴C₀ = 4! / (0! * 4!) = 1
- ⁴C₁ = 4! / (1! * 3!) = 4
- ⁴C₂ = 4! / (2! * 2!) = 6
- ⁴C₃ = 4! / (3! * 1!) = 4
- ⁴C₄ = 4! / (4! * 0!) = 1
Substituting the coefficients:
(a + b)^4 = 1 * a⁴b⁰ + 4 * a³b¹ + 6 * a²b² + 4 * a¹b³ + 1 * a⁰b⁴
Simplifying the expression:
(a + b)^4 = a⁴ + 4a³b + 6a²b² + 4ab³ + b⁴
Conclusion
The binomial theorem offers a systematic way to expand expressions of the form (a + b)^n. Understanding the pattern and applying the formula allows for efficient expansion of such expressions, which is crucial in various mathematical applications.