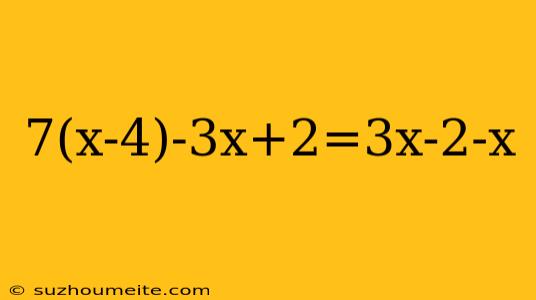Solving the Equation: 7(x-4)-3x+2=3x-2-x
In mathematics, equations are used to describe relationships between variables. Solving an equation means finding the value of the variable that makes the equation true. In this article, we will learn how to solve the equation 7(x-4)-3x+2=3x-2-x.
Step 1: Simplify the Left-Hand Side
The left-hand side of the equation is 7(x-4)-3x+2. To simplify it, we need to follow the order of operations (PEMDAS):
- Evaluate the expression inside the parentheses: x-4 = x - 4
- Multiply 7 by the expression: 7(x - 4) = 7x - 28
- Subtract 3x from the result: 7x - 28 - 3x = 4x - 28
- Add 2 to the result: 4x - 28 + 2 = 4x - 26
So, the simplified left-hand side is 4x - 26.
Step 2: Simplify the Right-Hand Side
The right-hand side of the equation is 3x-2-x. To simplify it, we can combine like terms:
- Subtract x from 3x: 3x - x = 2x
- Subtract 2 from the result: 2x - 2
So, the simplified right-hand side is 2x - 2.
Step 3: Equate the Two Expressions
Now that we have simplified both sides of the equation, we can equate them:
4x - 26 = 2x - 2
Step 4: Solve for x
To solve for x, we can add 26 to both sides of the equation:
4x - 26 + 26 = 2x - 2 + 26 4x = 2x + 24
Subtract 2x from both sides:
4x - 2x = 24 2x = 24
Divide both sides by 2:
x = 24/2 x = 12
Therefore, the value of x is 12.
Conclusion
In this article, we have learned how to solve the equation 7(x-4)-3x+2=3x-2-x. By simplifying both sides of the equation and solving for x, we found that the value of x is 12. This demonstrates the importance of following the order of operations and combining like terms when solving equations.