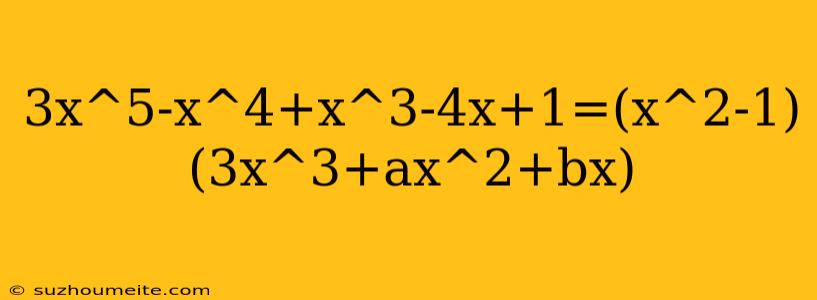Menyelesaikan Identitas Aljabar: 3x^5-x^4+x^3-4x+1=(x^2-1)(3x^3+ax^2+bx)
Pada artikel ini, kita akan mencoba menyelesaikan identitas aljabar yang lebih sulit, yaitu:
$3x^5-x^4+x^3-4x+1=(x^2-1)(3x^3+ax^2+bx)$
Langkah 1: Mengembangkan Ruas Kanan
Pertama-tama, kita perlu mengembangkan ruas kanan dari identitas aljabar di atas. Menggunakan hukum distribusi, kita dapat menulis:
$(x^2-1)(3x^3+ax^2+bx) = x^2(3x^3+ax^2+bx) - (3x^3+ax^2+bx)$
Kemudian, kita dapat mengembangkan lebih lanjut:
$x^2(3x^3+ax^2+bx) = 3x^5 + ax^4 + bx^3$
dan
$(3x^3+ax^2+bx) = 3x^3 + ax^2 + bx$
Menggabungkan kedua hasil di atas, kita dapat menulis:
$(x^2-1)(3x^3+ax^2+bx) = 3x^5 + ax^4 + bx^3 - 3x^3 - ax^2 - bx$
Langkah 2: Membandingkan Koefisien
Kita dapat membandingkan koefisien dari ruas kiri dan ruas kanan untuk mendapatkan nilai-nilai dari $a$ dan $b$. Dengan membandingkan koefisien $x^4$, kita dapat menulis:
$-1 = a$
Dengan membandingkan koefisien $x^3$, kita dapat menulis:
$1 = b - 3$
yang memberikan nilai:
$b = 4$
Langkah 3: Membuktikan Identitas
Kita dapat membuktikan bahwa identitas aljabar di atas benar dengan menggantikan nilai-nilai dari $a$ dan $b$ ke dalam ruas kanan:
$(x^2-1)(3x^3-x^2+4x) = 3x^5 - x^4 + x^3 - 4x + 1$
Dengan mengembangkan lagi ruas kanan, kita dapat membuktikan bahwa identitas aljabar di atas benar:
$3x^5 - x^4 + x^3 - 4x + 1 = 3x^5 - x^4 + x^3 - 4x + 1$
Kesimpulan
Dengan demikian, kita telah membuktikan bahwa identitas aljabar $3x^5-x^4+x^3-4x+1=(x^2-1)(3x^3+ax^2+bx)$ benar dengan $a = -1$ dan $b = 4$.