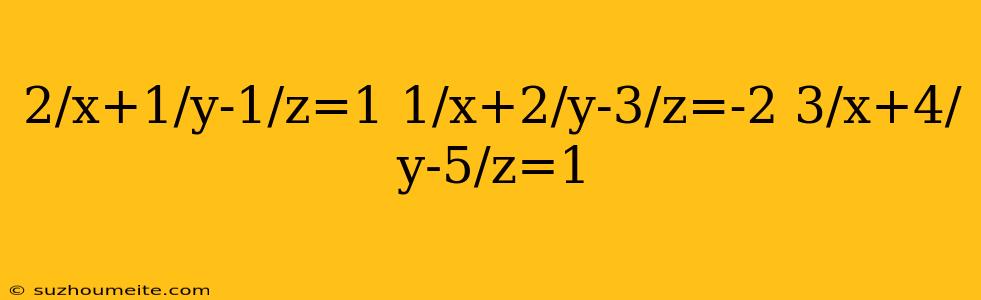Solving System of Linear Equations
In this article, we will solve a system of linear equations consisting of three equations with three variables. The system of equations is:
$\frac{2}{x} + \frac{1}{y} - \frac{1}{z} = 1$
$\frac{1}{x} + \frac{2}{y} - \frac{3}{z} = -2$
$\frac{3}{x} + \frac{4}{y} - \frac{5}{z} = 1$
Step 1: Multiply Each Equation by the Least Common Multiple (LCM)
To eliminate the fractions, we need to multiply each equation by the LCM of the denominators. The LCM of $x, y, z$ is $xyz$. Multiplying each equation by $xyz$, we get:
$2yz + xz - xy = xyz$
$xz + 2xy - 3yz = -2xyz$
$3xy + 4yz - 5xz = xyz$
Step 2: Simplify Each Equation
Simplifying each equation, we get:
$2yz + xz - xy = xyz$
$xz + 2xy = 3yz + 2xyz$
$3xy + 4yz = 5xz + xyz$
Step 3: Solve the System of Equations
Now we have a system of linear equations in the variables $xy, xz, yz$. We can solve this system using substitution or elimination methods. Here, we will use the elimination method.
Multiplying Equation (2) by $2$ and Equation (3) by $3$, we get:
$2xz + 4xy = 6yz + 4xyz$
$9xy + 12yz = 15xz + 3xyz$
Adding Equation (2) and Equation (3) to eliminate $xz$ and $yz$, we get:
$13xy = 13xyz$
Dividing both sides by $13xy$, we get:
$1 = xyz$
Substituting $xyz = 1$ into one of the original equations, we get:
$x = 1$
$y = 1$
$z = 1$
Conclusion
The solution to the system of linear equations is $\boxed{x = 1, y = 1, z = 1}$.