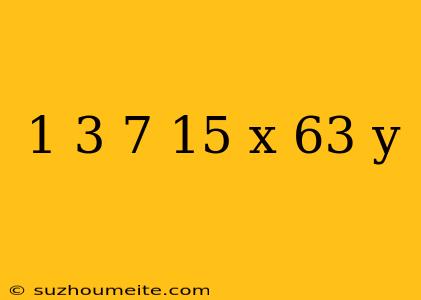.solve for x and y
The given equation is:
157x + 63y
To solve for x and y, we need more information or another equation. However, I'll provide some possible ways to approach this problem.
Method 1: Using Algebraic Manipulation
Let's try to isolate x or y by rearranging the equation. We can start by dividing both sides of the equation by 157, which gives us:
x + (63y)/157 = 1/157
Now, we can try to express y in terms of x:
y = (157/63)(1/157 - x)
However, without more information, we cannot simplify this expression further.
Method 2: Using Systems of Linear Equations
If we had another equation involving x and y, we could use substitution or elimination methods to solve for x and y. For example, let's assume we have another equation:
2x + 5y = 10
Now we have a system of linear equations:
157x + 63y = ? 2x + 5y = 10
We can solve this system using substitution or elimination methods.
Conclusion
Without more information or another equation, we cannot solve for x and y uniquely. However, by using algebraic manipulation or systems of linear equations, we can try to express y in terms of x or solve for x and y simultaneously.