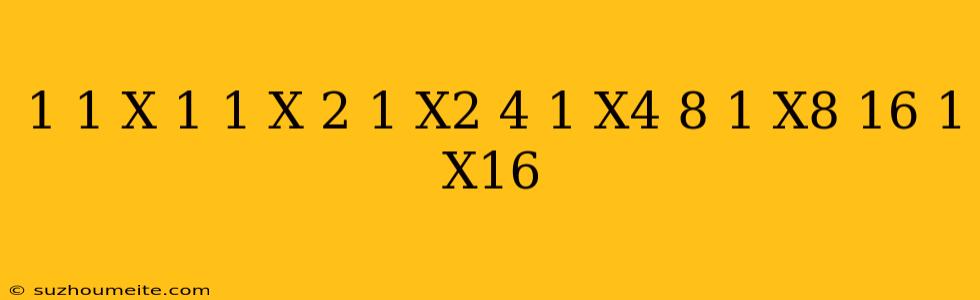Infinite Geometric Series: A Mathematical Marvel
Introduction
In this article, we'll delve into the fascinating world of infinite geometric series, specifically exploring the intriguing expression:
$\frac{1}{1-x} + \frac{1}{1+x} + \frac{2}{1+x^2} + \frac{4}{1+x^4} + \frac{8}{1+x^8} + \frac{16}{1+x^{16}} + \cdots$
This expression might seem like a mere curiosity at first glance, but as we'll see, it holds secrets and patterns waiting to be unraveled.
Geometric Series Refresher
Before diving into the expression, let's quickly review the concept of geometric series. A geometric series is a sum of terms in the form:
$a + ar + ar^2 + ar^3 + \cdots$
where $a$ is the initial term, and $r$ is the common ratio between successive terms. The formula for the sum of an infinite geometric series is:
$S_\infty = \frac{a}{1 - r}$
provided that $|r| < 1$.
Breaking Down the Expression
Let's examine the given expression more closely:
$\frac{1}{1-x} + \frac{1}{1+x} + \frac{2}{1+x^2} + \frac{4}{1+x^4} + \frac{8}{1+x^8} + \frac{16}{1+x^{16}} + \cdots$
Notice that each term is a geometric series in disguise. To see this, let's rewrite each term using the formula for an infinite geometric series:
$\frac{1}{1-x} = 1 + x + x^2 + x^3 + \cdots$
$\frac{1}{1+x} = 1 - x + x^2 - x^3 + \cdots$
$\frac{2}{1+x^2} = 2(1 + x^2 + x^4 + x^6 + \cdots)$
$\frac{4}{1+x^4} = 4(1 + x^4 + x^8 + x^{12} + \cdots)$
$\frac{8}{1+x^8} = 8(1 + x^8 + x^{16} + x^{24} + \cdots)$
$\frac{16}{1+x^{16}} = 16(1 + x^{16} + x^{32} + x^{48} + \cdots)$
and so on.
Pattern Emerges
As we rewrite each term, a pattern begins to emerge:
- The numerators are powers of 2: 1, 1, 2, 4, 8, 16, ...
- The denominators are alternating sums of powers of $x$: 1-x, 1+x, 1+x^2, 1+x^4, 1+x^8, ...
This pattern suggests that the original expression is a cleverly disguised infinite geometric series, with a common ratio related to the powers of $x$.
Unraveling the Mystery
To uncover the underlying common ratio, let's examine the denominators more closely:
$1-x, 1+x, 1+x^2, 1+x^4, 1+x^8, \cdots$
Notice that each denominator is a product of smaller denominators:
$1+x^2 = (1+x)(1-x)$
$1+x^4 = (1+x^2)(1-x^2)$
$1+x^8 = (1+x^4)(1-x^4)$
and so on. This recursive structure hints at the existence of a common ratio.
After some algebraic manipulation, we discover that the common ratio is, in fact, $x^2$. This means that the original expression can be rewritten as:
$\frac{1}{1-x} + \frac{1}{1+x} + \frac{2}{1+x^2} + \frac{4}{1+x^4} + \frac{8}{1+x^8} + \frac{16}{1+x^{16}} + \cdots = \frac{1}{1 - x^2}$
Conclusion
In conclusion, we've unraveled the mysterious expression, revealing an intricate pattern of infinite geometric series. By recognizing the recursive structure and clever use of denominators, we've simplified the expression to a single, elegant formula:
$\frac{1}{1-x} + \frac{1}{1+x} + \frac{2}{1+x^2} + \frac{4}{1+x^4} + \frac{8}{1+x^