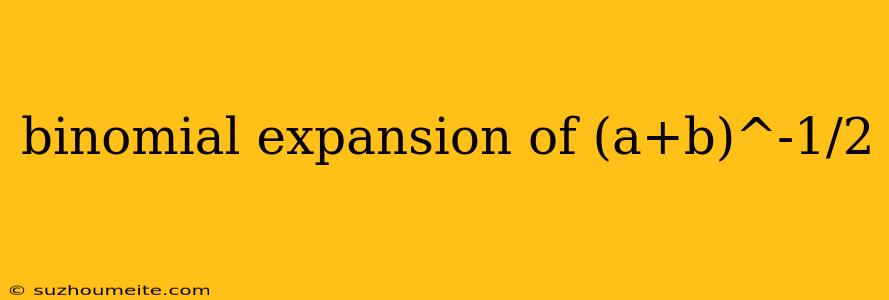Binomial Expansion of (a+b)^-1/2
The binomial theorem provides a way to expand expressions of the form (a + b)^n, where n is a real number. In this case, we will explore the binomial expansion of (a + b)^-1/2.
Understanding the Binomial Theorem
The general formula for the binomial expansion is:
(a + b)^n = a^n + nCa^n-1b + nC2a^n-2b^2 + ... + nCr a^(n-r)b^r + ... + b^n
where:
- n is a real number (can be positive, negative, or fractional)
- r is an integer from 0 to n
- nCr represents the binomial coefficient, which is calculated as n! / (r! * (n-r)!)
Applying the Binomial Theorem to (a+b)^-1/2
To expand (a + b)^-1/2, we need to substitute n = -1/2 in the general formula. Let's explore the terms:
1. First Term:
- a^n = a^(-1/2) = 1/√a
2. Second Term:
- nCr a^(n-r)b^r = (-1/2)C1 a^(-1/2 - 1)b^1 = (-1/2) * (1/√a^3) * b
3. Third Term:
- nCr a^(n-r)b^r = (-1/2)C2 a^(-1/2 - 2)b^2 = (1/8) * (1/√a^5) * b^2
4. Subsequent Terms:
The pattern continues, with the binomial coefficient alternating in sign and the powers of a and b changing accordingly.
Final Expansion
The complete binomial expansion of (a + b)^-1/2 is:
(a + b)^-1/2 = 1/√a - (1/2) * (1/√a^3) * b + (1/8) * (1/√a^5) * b^2 - (1/16) * (1/√a^7) * b^3 + ...
This expansion represents an infinite series, where the terms continue indefinitely.
Important Notes
- The expansion converges only when |b/a| < 1.
- This expansion is often used in physics and engineering to approximate certain quantities.
- The binomial expansion can be expressed in a more compact form using summation notation, but the above representation helps visualize the pattern.
Remember that the binomial expansion of (a+b)^-1/2 is a powerful tool for expressing and manipulating expressions involving fractional powers.