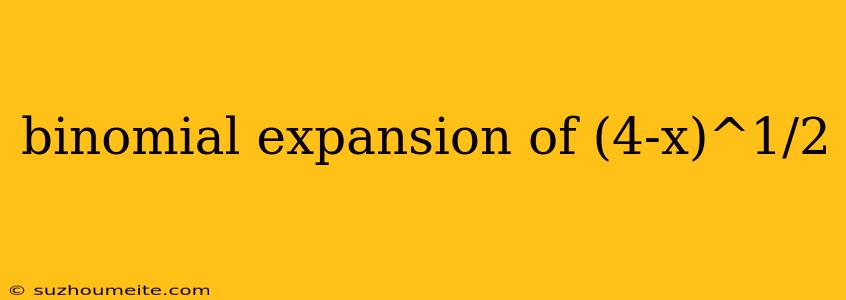Binomial Expansion of (4 - x)^1/2
The binomial theorem allows us to expand expressions of the form (a + b)^n, where n is a real number. We can use this theorem to expand (4 - x)^1/2.
Here's how:
1. Identify 'a' and 'b'
In our expression, (4 - x)^1/2:
- a = 4
- b = -x
2. Apply the Binomial Theorem
The general formula for the binomial theorem is:
(a + b)^n = a^n + nCa * a^(n-1) * b + nC2 * a^(n-2) * b^2 + ... + nCn * b^n
Where nCr represents the binomial coefficient, calculated as n! / (r! * (n-r)!).
3. Expand (4 - x)^1/2
Let's apply the formula to our expression:
(4 - x)^1/2 = 4^(1/2) + (1/2)C1 * 4^(1/2 - 1) * (-x) + (1/2)C2 * 4^(1/2 - 2) * (-x)^2 + ...
4. Simplify the Expression
Simplifying the terms:
- 4^(1/2) = 2
- (1/2)C1 = (1/2)! / (1! * (1/2 - 1)!) = -1/2
- (1/2)C2 = (1/2)! / (2! * (1/2 - 2)!) = 1/8
- ...
Therefore, the expansion becomes:
(4 - x)^1/2 = 2 - (1/2) * x + (1/8) * x^2 - (1/16) * x^3 + ...
5. Finding the Pattern
Notice a pattern emerges in the coefficients:
- The first term is 2.
- The coefficient of the x term is -1/2.
- The coefficient of the x^2 term is (1/2) * (-1/2) / 2 = 1/8.
- The coefficient of the x^3 term is (1/8) * (-1/2) / 3 = -1/16.
This pattern continues, alternating between positive and negative values.
6. The Valid Range
The binomial expansion for (4 - x)^1/2 is valid for |x| < 4. This is because the expansion involves terms with powers of x, and for large values of x, the series diverges and doesn't converge to a finite value.
Conclusion
The binomial expansion of (4 - x)^1/2 is a useful tool for representing this expression as an infinite series. It provides an accurate approximation for values of x within a certain range. This expansion has applications in various fields like calculus, statistics, and physics.