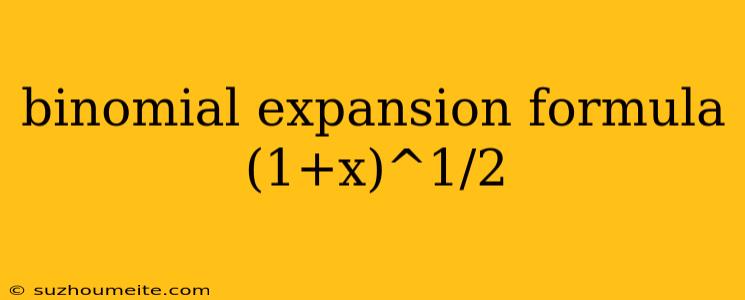Binomial Expansion Formula for (1 + x)^(1/2)
The binomial theorem provides a formula for expanding expressions of the form (a + b)^n, where n is a positive integer. However, this formula can be extended to cases where n is a rational number, including fractional powers. This article will delve into the binomial expansion formula for (1 + x)^(1/2), also known as the square root of (1 + x).
The Binomial Theorem for Fractional Powers
The generalized binomial theorem states that for any real number n, and for |x| < 1, the following expansion holds:
(1 + x)^n = 1 + nx + (n(n-1)/2!)x² + (n(n-1)(n-2)/3!)x³ + ...
This infinite series is called the binomial series.
Applying the Formula to (1 + x)^(1/2)
Let's substitute n = 1/2 into the binomial series formula:
(1 + x)^(1/2) = 1 + (1/2)x + ((1/2)(-1/2)/2!)x² + ((1/2)(-1/2)(-3/2)/3!)x³ + ...
Simplifying the coefficients, we get:
(1 + x)^(1/2) = 1 + (1/2)x - (1/8)x² + (1/16)x³ - (5/128)x⁴ + ...
Understanding the Expansion
This expansion represents the square root of (1 + x) as an infinite series of terms. Each term has a coefficient that is a combination of the fractional power (1/2) and the corresponding power of x.
Limitations and Applications
This expansion is valid for |x| < 1. This means the formula works accurately when the absolute value of x is less than 1. For values of x outside this range, the series may diverge.
The binomial expansion formula for (1 + x)^(1/2) has numerous applications in various fields, including:
- Calculus: Finding derivatives and integrals of functions involving square roots.
- Physics: Calculating quantities related to motion, gravity, and other physical phenomena.
- Statistics: Working with probability distributions and statistical models.
Conclusion
The binomial expansion formula provides a powerful tool for expressing the square root of (1 + x) as an infinite series. It allows us to approximate the value of this expression for certain values of x and has wide-ranging applications in different fields. By understanding the formula and its limitations, we can effectively utilize it for various mathematical and scientific tasks.