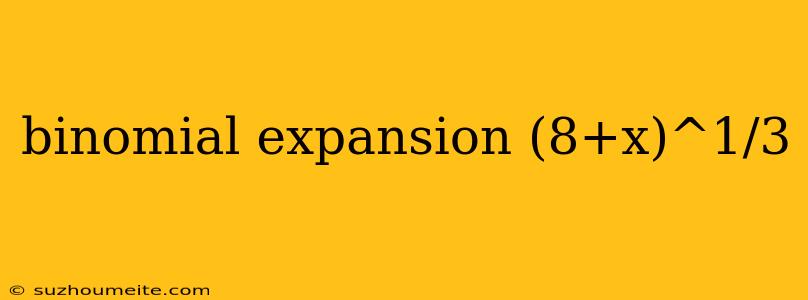Binomial Expansion of (8+x)^(1/3)
The binomial theorem allows us to expand expressions of the form (a + x)^n, where n is a rational number. In this case, we'll explore the expansion of (8 + x)^(1/3).
Understanding the Binomial Theorem
The binomial theorem states:
(a + x)^n = a^n + (n choose 1) * a^(n-1) * x + (n choose 2) * a^(n-2) * x^2 + ... + (n choose r) * a^(n-r) * x^r + ... + x^n
where:
- (n choose r) represents the binomial coefficient, calculated as n! / (r! * (n-r)!).
Applying the Theorem to (8 + x)^(1/3)
-
Identify a and x: In our case, a = 8 and x = x.
-
Determine n: Here, n = 1/3.
-
Calculate binomial coefficients: We'll need to calculate the binomial coefficients for each term in the expansion.
- (1/3 choose 0) = 1
- (1/3 choose 1) = 1/3
- (1/3 choose 2) = -1/9
- (1/3 choose 3) = 1/27
- And so on...
-
Substitute values into the binomial theorem formula:
(8 + x)^(1/3) = 8^(1/3) + (1/3 choose 1) * 8^(1/3 - 1) * x + (1/3 choose 2) * 8^(1/3 - 2) * x^2 + (1/3 choose 3) * 8^(1/3 - 3) * x^3 + ...
- Simplify the terms:
(8 + x)^(1/3) = 2 + (1/3) * 2^(-2/3) * x - (1/9) * 2^(-5/3) * x^2 + (1/27) * 2^(-8/3) * x^3 + ...
The Resulting Expansion
Therefore, the binomial expansion of (8 + x)^(1/3) is:
(8 + x)^(1/3) = 2 + (1/3) * 2^(-2/3) * x - (1/9) * 2^(-5/3) * x^2 + (1/27) * 2^(-8/3) * x^3 + ...
This expansion will continue infinitely, but the terms will become increasingly smaller as the power of x increases.
Note
This expansion is valid for values of x where |x/8| < 1. This ensures that the series converges to a finite value.