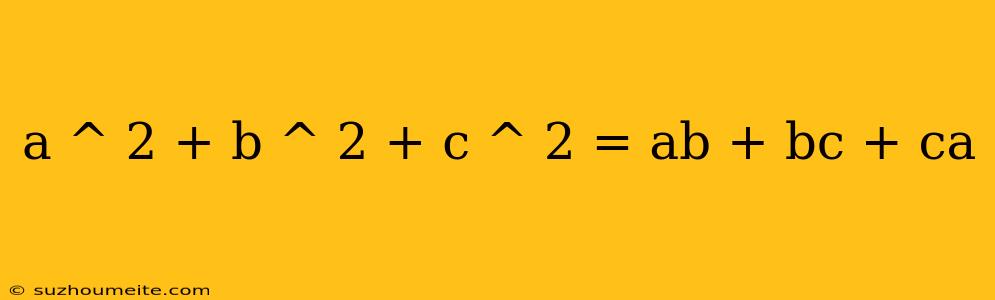Menjelajahi Persamaan: a² + b² + c² = ab + bc + ca
Persamaan a² + b² + c² = ab + bc + ca adalah sebuah persamaan yang menarik dan memiliki beberapa aplikasi dalam berbagai bidang matematika. Artikel ini akan membahas lebih dalam tentang persamaan ini, termasuk:
1. Menganalisis Persamaan
Persamaan ini dapat diinterpretasikan dalam beberapa cara:
- Persamaan Simetris: Persamaan ini simetris terhadap variabel a, b, dan c. Artinya, jika kita menukar posisi variabel-variabel tersebut, persamaan tetap berlaku.
- Persamaan Kuadrat: Persamaan ini dapat ditulis sebagai persamaan kuadrat dalam variabel a, b, atau c. Misalnya, jika kita ingin menyelesaikan persamaan untuk variabel a, kita bisa menuliskannya sebagai: a² - (b + c)a + (b² + c² - bc) = 0.
2. Mencari Solusi
Persamaan ini memiliki beberapa solusi:
- Solusi Sepele: a = b = c. Jika ketiga variabel memiliki nilai yang sama, persamaan tersebut terpenuhi.
- Solusi Lain: Persamaan ini juga memiliki solusi lain yang bisa diperoleh melalui pemfaktoran atau metode lain penyelesaian persamaan kuadrat.
3. Penerapan dalam Geometri
Persamaan ini memiliki aplikasi dalam geometri, terutama dalam:
- Segitiga: Persamaan ini terkait dengan Teorema Pythagoras dan Hukum Cosinus. Misalnya, jika kita memiliki segitiga dengan sisi a, b, dan c, dan sudut C yang berhadapan dengan sisi c, maka persamaan ini dapat ditulis sebagai: c² = a² + b² - 2ab cos C. Jika cos C = 1/2 (yang berlaku untuk segitiga sama kaki), maka persamaan ini akan sama dengan persamaan awal.
- Lingkaran: Persamaan ini juga terkait dengan persamaan lingkaran. Misalnya, jika kita memiliki lingkaran dengan pusat (h, k) dan jari-jari r, maka persamaan lingkaran tersebut dapat ditulis sebagai: (x - h)² + (y - k)² = r². Persamaan awal dapat diinterpretasikan sebagai persamaan lingkaran dengan pusat (0, 0) dan jari-jari √(ab + bc + ca).
4. Penerapan dalam Aljabar
Persamaan ini memiliki aplikasi dalam aljabar, terutama dalam:
- Pemfaktoran: Persamaan ini dapat difaktorkan menjadi: (a - b)² + (b - c)² + (c - a)² = 0. Persamaan ini menunjukkan bahwa jika a = b = c, maka persamaan awal terpenuhi.
- Identitas Trigonometri: Persamaan ini juga dapat dihubungkan dengan beberapa identitas trigonometri. Misalnya, dengan menggunakan identitas cos 2θ = 1 - 2sin²θ, kita dapat menulis persamaan awal sebagai: sin²(a - b) + sin²(b - c) + sin²(c - a) = 0.
5. Pembahasan Lanjut
Persamaan a² + b² + c² = ab + bc + ca merupakan persamaan yang menarik dan memiliki banyak aplikasi. Pembahasan lebih lanjut mengenai persamaan ini bisa meliputi:
- Solusi Kompleks: Persamaan ini memiliki solusi kompleks, selain solusi real yang telah dibahas sebelumnya.
- Relasi dengan Persamaan Lainnya: Persamaan ini dapat dihubungkan dengan berbagai persamaan matematika lainnya, seperti persamaan kubik atau persamaan matriks.
- Aplikasi dalam Bidang Lainnya: Persamaan ini memiliki aplikasi dalam bidang lain seperti fisika, kimia, dan ekonomi.
Melalui analisis, pencarian solusi, dan penerapannya, persamaan ini membuka pintu menuju pemahaman yang lebih dalam tentang berbagai konsep matematika dan aplikasinya di dunia nyata.