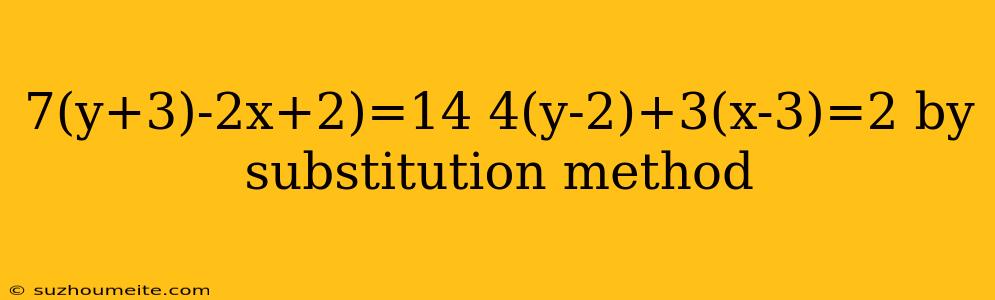Solving Systems of Linear Equations using Substitution Method
In this article, we will solve a system of linear equations using the substitution method. The system of equations is:
Equation 1: 7(y + 3) - 2x + 2 = 14 Equation 2: 4(y - 2) + 3(x - 3) = 2
Step 1: Simplify the Equations
Let's simplify both equations by combining like terms:
Equation 1: 7y + 21 - 2x + 2 = 14 => 7y - 2x + 23 = 14 => 7y - 2x = -9 ... (1)
Equation 2: 4y - 8 + 3x - 9 = 2 => 4y + 3x - 17 = 2 => 4y + 3x = 19 ... (2)
Step 2: Solve One of the Equations for One Variable
Let's solve Equation (1) for y:
7y - 2x = -9 => 7y = 2x - 9 => y = (2x - 9) / 7 ... (3)
Step 3: Substitute the Expression into the Other Equation
Now, substitute the expression for y from Equation (3) into Equation (2):
4((2x - 9) / 7) + 3x = 19
Step 4: Simplify and Solve for x
Simplify the equation by multiplying both sides by 7:
4(2x - 9) + 21x = 133 => 8x - 36 + 21x = 133 => 29x = 169 => x = 169 / 29 => x = 5.83 (approx.)
Step 5: Substitute the Value of x into One of the Original Equations to Solve for y
Now that we have the value of x, substitute it into Equation (3) to solve for y:
y = (2(5.83) - 9) / 7 => y = (11.66 - 9) / 7 => y = 2.66 / 7 => y = 0.38 (approx.)
Solution
The solution to the system of equations is x = 5.83 and y = 0.38.