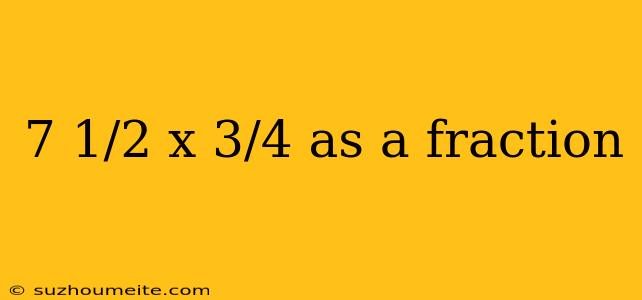7 1/2 x 3/4 as a Fraction
In this article, we will explore how to multiply mixed numbers, specifically the problem 7 1/2 x 3/4 as a fraction.
Understanding Mixed Numbers
Before we dive into the problem, let's quickly review what mixed numbers are. A mixed number is a combination of a whole number and a fraction. For example, 7 1/2 is a mixed number, where 7 is the whole number and 1/2 is the fraction.
Converting Mixed Numbers to Improper Fractions
To multiply mixed numbers, we need to convert them to improper fractions first. An improper fraction is a fraction where the numerator is greater than the denominator.
To convert 7 1/2 to an improper fraction, we can follow these steps:
- Multiply the whole number part (7) by the denominator (2): 7 × 2 = 14
- Add the numerator (1) to the product: 14 + 1 = 15
- Write the result as an improper fraction: 15/2
So, 7 1/2 = 15/2.
Converting the Second Mixed Number
Let's convert the second mixed number, 3/4, to an improper fraction:
- 3/4 is already an improper fraction, so we don't need to do anything.
Multiplying the Fractions
Now that we have the improper fractions, we can multiply them:
- Multiply the numerators (15 × 3 = 45)
- Multiply the denominators (2 × 4 = 8)
- Write the result as a fraction: 45/8
Simplifying the Fraction
We can simplify the fraction 45/8 by dividing both the numerator and the denominator by their greatest common divisor (GCD). The GCD of 45 and 8 is 1, so the fraction is already in its simplest form.
The Final Answer
So, 7 1/2 x 3/4 as a fraction is equal to 45/8.
I hope this article has helped you understand how to multiply mixed numbers and convert them to improper fractions. If you have any more questions or need further clarification, feel free to ask!