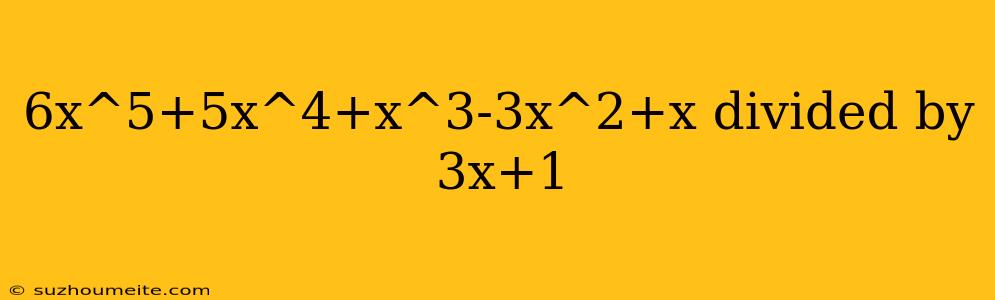Polynomial Long Division: 6x^5+5x^4+x^3-3x^2+x divided by 3x+1
In this article, we will perform polynomial long division to divide the polynomial 6x^5+5x^4+x^3-3x^2+x by 3x+1.
Step 1: Write the dividend and divisor
The dividend is the polynomial being divided, which is 6x^5+5x^4+x^3-3x^2+x. The divisor is the polynomial by which we are dividing, which is 3x+1.
Step 2: Divide the leading terms
To divide the leading terms, we need to find the quotient of the leading terms of the dividend and divisor. In this case, the leading terms are 6x^5 and 3x. The quotient of these terms is 2x^4.
Step 3: Multiply the divisor by the quotient and subtract
Multiply the divisor 3x+1 by the quotient 2x^4 and subtract the result from the dividend.
2x^4
3x+1 ) 6x^5 + 5x^4 + x^3 - 3x^2 + x
- (6x^5 + 2x^4)
Step 4: Bring down the next term and repeat
Bring down the next term of the dividend and repeat steps 2 and 3.
2x^4 + 1x^3
3x+1 ) 6x^5 + 5x^4 + x^3 - 3x^2 + x
- (6x^5 + 2x^4)
3x^4 + x^3 - 3x^2 + x
- (3x^4 + 1x^3)
-2x^2 + x
Step 5: Repeat the process until the remainder is zero or has a smaller degree than the divisor
Continue repeating steps 2-4 until the remainder is zero or has a smaller degree than the divisor.
2x^4 + 1x^3 - 1x
3x+1 ) 6x^5 + 5x^4 + x^3 - 3x^2 + x
- (6x^5 + 2x^4)
3x^4 + x^3 - 3x^2 + x
- (3x^4 + 1x^3)
-2x^2 + x
- (-2x^2 - 2x)
3x + 1
- (3x + 1)
0
The final result
The final result of the polynomial long division is:
Quotient: 2x^4 + 1x^3 - 1x Remainder: 0
Therefore, we have successfully divided the polynomial 6x^5+5x^4+x^3-3x^2+x by 3x+1 using polynomial long division.