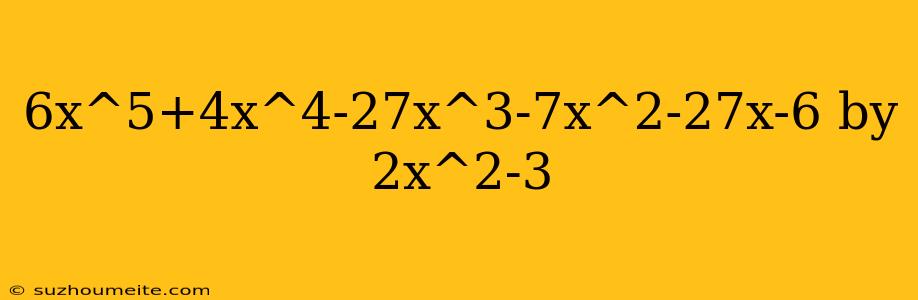Division of Polynomials: 6x^5+4x^4-27x^3-7x^2-27x-6 by 2x^2-3
In this article, we will discuss the division of polynomials, specifically the division of the polynomial 6x^5+4x^4-27x^3-7x^2-27x-6 by 2x^2-3.
The Division Algorithm
The division algorithm is a method for dividing one polynomial by another and obtaining the quotient and remainder. It is similar to the long division method used for dividing numbers.
Step-by-Step Division
To divide the polynomial 6x^5+4x^4-27x^3-7x^2-27x-6 by 2x^2-3, we will follow the steps below:
Step 1: Write the dividend and divisor
The dividend is the polynomial being divided, which is 6x^5+4x^4-27x^3-7x^2-27x-6. The divisor is the polynomial by which we are dividing, which is 2x^2-3.
Step 2: Divide the leading term of the dividend by the leading term of the divisor
The leading term of the dividend is 6x^5, and the leading term of the divisor is 2x^2. To divide these terms, we need to find the term that, when multiplied by 2x^2, gives us 6x^5. This term is 3x^3.
Step 3: Multiply the divisor by the term found in step 2 and subtract the product from the dividend
Multiply 2x^2-3 by 3x^3 to get 6x^5 - 9x^3. Subtract this product from the dividend to get:
4x^4 - 18x^3 - 7x^2 - 27x - 6
Step 4: Repeat steps 2 and 3 with the remaining terms
The remaining terms are 4x^4 - 18x^3 - 7x^2 - 27x - 6. The leading term of this polynomial is 4x^4. Divide this term by the leading term of the divisor (2x^2) to get 2x^2.
Multiply 2x^2-3 by 2x^2 to get 4x^4 - 6x^2. Subtract this product from the remaining terms to get:
- 12x^3 - x^2 - 27x - 6
Step 5: Repeat steps 2 and 3 until the remainder has a degree less than the divisor
Repeat steps 2 and 3 with the remaining terms until the remainder has a degree less than the divisor.
The final result is:
Quotient: 3x^3 + 2x^2 - 6
Remainder: -27x - 6
Therefore, the division of the polynomial 6x^5+4x^4-27x^3-7x^2-27x-6 by 2x^2-3 gives us a quotient of 3x^3 + 2x^2 - 6 and a remainder of -27x - 6.