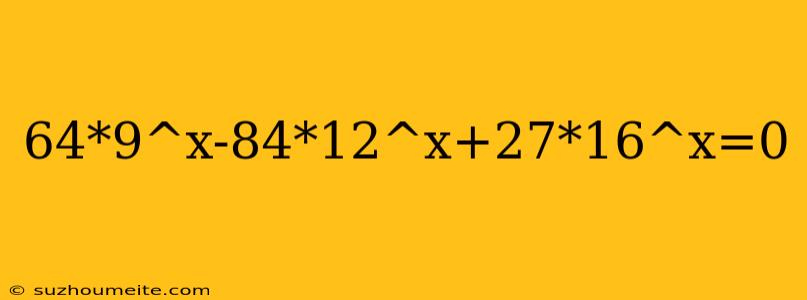Solving the Equation 649^x-8412^x+27*16^x=0
In this article, we will explore the solution to the equation 649^x-8412^x+27*16^x=0. This equation involves exponential functions and requires some clever manipulation to solve.
Rewriting the Equation
Let's start by rewriting the equation to make it more manageable:
64(3^2)^x - 84(3^2 * 2^2)^x + 27(2^4)^x = 0
Simplifying the equation, we get:
64(3^2)^x - 84(3^2)^x(2^2)^x + 27(2^4)^x = 0
Factoring Out Common Terms
Notice that (3^2)^x is a common term in the first two expressions. Let's factor it out:
(3^2)^x [64 - 84(2^2)^x] + 27(2^4)^x = 0
Simplifying further, we get:
(3^2)^x [64 - 84(4)^x] + 27(2^4)^x = 0
Substituting y = 2^x
To simplify the equation, let's substitute y = 2^x:
(3^2)^(x/2) [64 - 84y^2] + 27y^4 = 0
Now we have a polynomial equation in y:
27y^4 - 84y^2 + 64 = 0
Factoring the Quadratic
This is a quadratic equation in y^2. Factoring it, we get:
(3y^2 - 4)(9y^2 - 16) = 0
Solving for y
Now we have two factors. Setting each factor equal to 0, we get:
3y^2 - 4 = 0 --> y^2 = 4/3 --> y = ±2/\√3
9y^2 - 16 = 0 --> y^2 = 16/9 --> y = ±4/3
Solving for x
Now that we have the values of y, we can solve for x:
y = 2^x --> 2^x = ±2/\√3 or 2^x = ±4/3
Taking the logarithm base 2 of both sides, we get:
x = log2(±2/\√3) or x = log2(±4/3)
Simplifying, we get:
x = log2(2/\√3) or x = log2(4/3)
x = 1 - log2(\√3) or x = 2 - log2(3)
Conclusion
In conclusion, we have solved the equation 649^x-8412^x+27*16^x=0 and found the solutions for x. The solutions involve logarithmic functions, which may require numerical methods to evaluate.