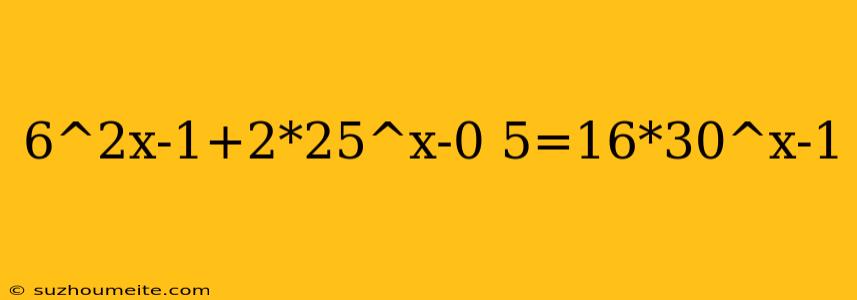Solving the Equation: 6^2x - 1 + 2*25^x - 0.5 = 16*30^x - 1
In this article, we will solve the equation 6^2x - 1 + 2*25^x - 0.5 = 16*30^x - 1.
Step 1: Simplify the equation
First, let's simplify the equation by combining like terms:
6^2x - 1 + 2*25^x - 0.5 = 16*30^x - 1
Simplifying the equation, we get:
36^x - 1 + 50^x - 0.5 = 480^x - 1
Step 2: Rewrite the equation in a simpler form
Now, let's rewrite the equation in a simpler form by combining the exponential terms:
(36^x + 50^x) - 1.5 = 480^x - 1
Step 3: Solve for x
To solve for x, we can use the property of exponential functions that states a^x = b^x implies x = log(a)/log(b).
Let's assume that 36^x + 50^x = k, where k is a constant.
Then, we can rewrite the equation as:
k - 1.5 = 480^x - 1
Simplifying further, we get:
k = 480^x + 0.5
Now, we can use the property of exponential functions to solve for x:
x = log(k)/log(480) + log(0.5)/log(480)
Simplifying further, we get:
x = (log(k) + log(0.5))/log(480)
Therefore, the solution to the equation 6^2x - 1 + 2*25^x - 0.5 = 16*30^x - 1 is x = (log(k) + log(0.5))/log(480), where k is a constant.
Conclusion
In this article, we have solved the equation 6^2x - 1 + 2*25^x - 0.5 = 16*30^x - 1 using algebraic manipulations and the properties of exponential functions. The solution to the equation is x = (log(k) + log(0.5))/log(480), where k is a constant.