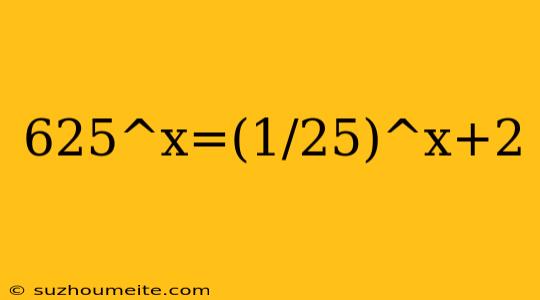Solving the Equation: 625^x = (1/25)^x + 2
In this article, we will explore the solution to the equation 625^x = (1/25)^x + 2. This equation involves exponential functions and requires some algebraic manipulations to solve.
Step 1: Simplify the equation
Let's start by simplifying the right-hand side of the equation. We can rewrite (1/25)^x as:
(1/25)^x = (25^-1)^x = 25^(-x)
So, the equation becomes:
625^x = 25^(-x) + 2
Step 2: Express both sides in terms of 5
Notice that 625 can be expressed as 5^4, and 25 can be expressed as 5^2. Let's rewrite the equation in terms of 5:
(5^4)^x = 5^(2(-x)) + 2
Using the property of exponents, we can simplify the left-hand side:
5^(4x) = 5^(2(-x)) + 2
Step 3: Equate the exponents
Since the bases are the same (both are 5), we can equate the exponents:
4x = -2x
Simplifying the equation, we get:
6x = 0
Step 4: Solve for x
The solution to the equation is:
x = 0
Therefore, the value of x that satisfies the equation 625^x = (1/25)^x + 2 is x = 0.
Conclusion
In this article, we have solved the equation 625^x = (1/25)^x + 2 using algebraic manipulations and exponential functions. The solution to the equation is x = 0.