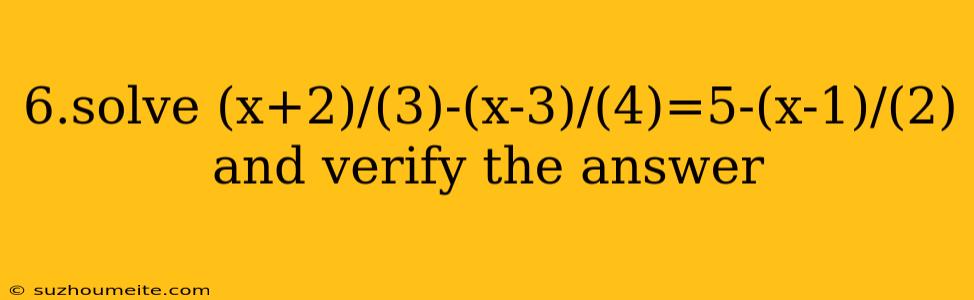Solving the Equation
Problem Statement
Solve the equation:
$\frac{x+2}{3} - \frac{x-3}{4} = 5 - \frac{x-1}{2}$
Solution
To solve this equation, we can start by combining the fractions on the left-hand side:
$\frac{x+2}{3} - \frac{x-3}{4} = \frac{4(x+2) - 3(x-3)}{12}$
Simplifying the numerator, we get:
$\frac{4x + 8 - 3x + 9}{12} = \frac{x + 17}{12}$
Now, we can equate this expression to the right-hand side of the original equation:
$\frac{x + 17}{12} = 5 - \frac{x-1}{2}$
Multiplying both sides by 12 to eliminate the fraction, we get:
$x + 17 = 60 - 6x + 6$
Combine like terms:
$7x = 49$
Dividing both sides by 7, we get:
$x = \boxed{7}$
Verifying the Answer
To verify our answer, we can plug $x = 7$ back into the original equation:
$\frac{7+2}{3} - \frac{7-3}{4} = 5 - \frac{7-1}{2}$
Simplifying, we get:
$\frac{9}{3} - \frac{4}{4} = 5 - \frac{6}{2}$
$3 - 1 = 5 - 3$
$2 = 2$
The equation holds true, which means our solution $x = 7$ is correct!
Therefore, the solution to the equation is $x = \boxed{7}$.