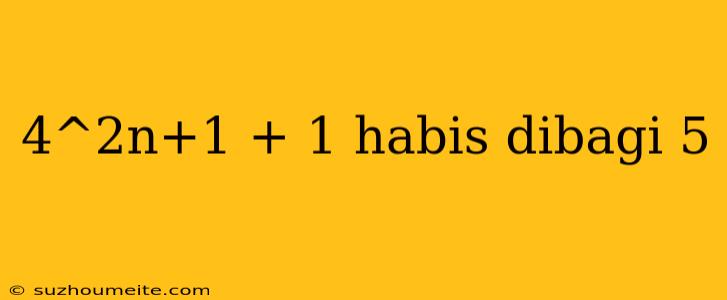Bukti bahwa 4^2n+1 + 1 Habis Dibagi 5
Pada artikel ini, kita akan membuktikan bahwa untuk setiap bilangan bulat non-negatif $n$, maka $4^{2n+1} + 1$ habis dibagi 5.
Teorema
$4^{2n+1} + 1 \equiv 0 \pmod{5}$
Bukti
Untuk membuktikan teorema di atas, kita dapat menggunakan induksi matematika.
Basis
Untuk $n = 0$, kita memiliki:
$4^{2\cdot0+1} + 1 = 4^1 + 1 = 5$
Dengan demikian, kita dapat melihat bahwa $4^{2\cdot0+1} + 1$ memang habis dibagi 5.
Induksi
Asumsikan bahwa untuk suatu bilangan bulat non-negatif $k$, maka $4^{2k+1} + 1 \equiv 0 \pmod{5}$. Kita harus membuktikan bahwa jika asumsi tersebut benar, maka juga berlaku untuk $k+1$, yaitu:
$4^{2(k+1)+1} + 1 \equiv 0 \pmod{5}$
Perhitungan
$4^{2(k+1)+1} + 1 = 4^{2k+3} + 1$
$= 4^2 \cdot 4^{2k+1} + 1$
$= 16 \cdot 4^{2k+1} + 1$
Karena kita mengasumsikan bahwa $4^{2k+1} + 1 \equiv 0 \pmod{5}$, maka kita dapat menulis:
$4^{2k+1} + 1 = 5m, \quad m \in \mathbb{Z}$
Dengan demikian, kita dapat mentransformasikan persamaan sebelumnya menjadi:
$16 \cdot 4^{2k+1} + 1 = 16 \cdot (5m - 1) + 1$
$= 80m - 16 + 1$
$= 80m - 15$
$= 5(16m - 3)$
Dengan demikian, kita dapat melihat bahwa $4^{2(k+1)+1} + 1 \equiv 0 \pmod{5}$, sehingga membuktikan bahwa teorema tersebut benar untuk $k+1$.
Kesimpulan
Dengan menggunakan induksi matematika, kita telah membuktikan bahwa untuk setiap bilangan bulat non-negatif $n$, maka $4^{2n+1} + 1 \equiv 0 \pmod{5}$, atau dengan kata lain, $4^{2n+1} + 1$ habis dibagi 5.