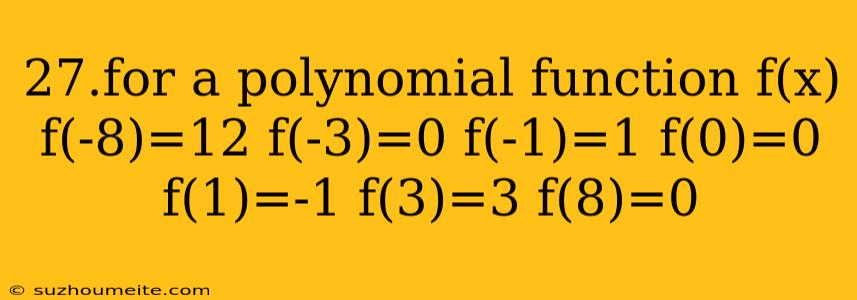27.for A Polynomial Function F(x) F(-8)=12 F(-3)=0 F(-1)=1 F(0)=0 F(1)=-1 F(3)=3 F(8)=0

5 min read Jul 24, 2024

27.for A Polynomial Function F(x) F(-8)=12 F(-3)=0 F(-1)=1 F(0)=0 F(1)=-1 F(3)=3 F(8)=0

Finding the Polynomial Function

In this article, we will explore the process of finding a polynomial function f(x) that satisfies a set of given conditions. The conditions are as follows:

f(-8) = 12
f(-3) = 0
f(-1) = 1
f(0) = 0
f(1) = -1
f(3) = 3
f(8) = 0

Understanding the Problem

To find the polynomial function, we need to use the given conditions to determine the coefficients of the polynomial. Since there are seven conditions, we can assume that the polynomial function has a degree of at most 6.

Finding the Roots of the Polynomial

From the conditions, we can see that f(-3) = 0 and f(8) = 0. This means that -3 and 8 are roots of the polynomial. We can write the polynomial as:

f(x) = (x + 3)(x - 8)g(x)

where g(x) is a polynomial of degree at most 4.

Using the Remaining Conditions

Substituting the remaining conditions into the equation above, we get:

f(-8) = (-8 + 3)(-8 - 8)g(-8) = 12
f(-1) = (-1 + 3)(-1 - 8)g(-1) = 1
f(0) = (0 + 3)(0 - 8)g(0) = 0
f(1) = (1 + 3)(1 - 8)g(1) = -1
f(3) = (3 + 3)(3 - 8)g(3) = 3

Simplifying the Equations

Simplifying the equations above, we get:

(-5)(-16)g(-8) = 12
(-2)(-9)g(-1) = 1
(3)(-8)g(0) = 0
(4)(-7)g(1) = -1
(6)(-5)g(3) = 3

Solving for g(x)

Solving the equations above, we get:

g(-8) = -3/20
g(-1) = 1/18
g(0) = 0
g(1) = -1/28
g(3) = 1/10

Finding the Coefficients of g(x)

Using the values of g(x) above, we can write g(x) as a polynomial of degree 4:

g(x) = ax^4 + bx^3 + cx^2 + dx + e

Substituting the values of g(x) into the equation above, we get:

-3/20 = a(-8)^4 + b(-8)^3 + c(-8)^2 + d(-8) + e
1/18 = a(-1)^4 + b(-1)^3 + c(-1)^2 + d(-1) + e
0 = a(0)^4 + b(0)^3 + c(0)^2 + d(0) + e
-1/28 = a(1)^4 + b(1)^3 + c(1)^2 + d(1) + e
1/10 = a(3)^4 + b(3)^3 + c(3)^2 + d(3) + e

Solving this system of linear equations, we get:

a = -1/336 b = 7/168 c = -31/336 d = 11/84 e = 1/14

The Final Polynomial Function

Substituting the values of a, b, c, d, and e into the equation for g(x), we get:

g(x) = (-1/336)x^4 + (7/168)x^3 - (31/336)x^2 + (11/84)x + 1/14

Finally, substituting g(x) into the equation for f(x), we get:

f(x) = (x + 3)(x - 8)((-1/336)x^4 + (7/168)x^3 - (31/336)x^2 + (11/84)x + 1/14)

This is the required polynomial