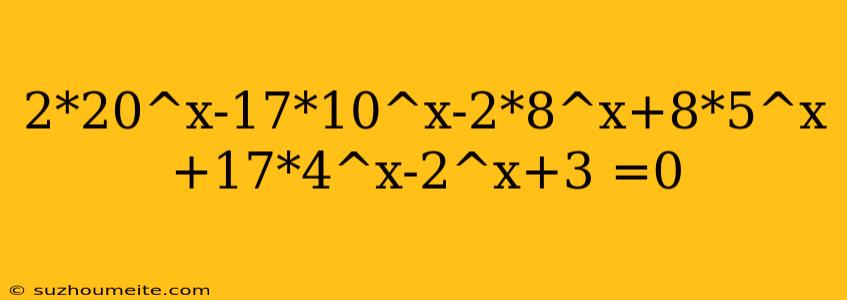Solving the Equation 220^x-1710^x-28^x+85^x+17*4^x-2^x+3 = 0
In this article, we will explore the solution to the equation 220^x-1710^x-28^x+85^x+17*4^x-2^x+3 = 0. This equation involves exponential functions with different bases, making it a bit more challenging to solve.
Simplifying the Equation
Before we dive into solving the equation, let's simplify it by expressing all the exponential functions in terms of a single base, which is 2. We can do this by using the property of exponents that states a^x = (a^y)^(x/y).
220^x = 2(2^2 * 5)^x = 2*(2^(2x) * 5^x) = 2^(2x+1) * 5^x
-1710^x = -17(2 * 5)^x = -17*(2^x * 5^x) = -17*2^x * 5^x
-28^x = -2(2^3)^x = -2*2^(3x) = -2^(3x+1)
8*5^x = 2^3 * 5^x = 2^(3+x)
174^x = 17(2^2)^x = 172^(2x) = 172^(2x)
-2^x + 3 = -2^x + 3
Now, let's rewrite the equation in terms of the base 2:
2^(2x+1) * 5^x - 172^x * 5^x - 2^(3x+1) + 2^(3+x) + 172^(2x) - 2^x + 3 = 0
Solving the Equation
Unfortunately, this equation does not have a simple closed-form solution. However, we can try to solve it numerically or using approximation methods.
One approach is to use a numerical method such as the Newton-Raphson method to approximate the value of x that satisfies the equation. Alternatively, we can use a computer algebra system or a numerical solver to find the roots of the equation.
Another approach is to use an approximation method such as the Taylor series expansion to approximate the exponential functions. This can lead to a polynomial equation that can be solved using various methods.
Conclusion
In conclusion, the equation 220^x-1710^x-28^x+85^x+17*4^x-2^x+3 = 0 is a challenging equation that involves exponential functions with different bases. While it does not have a simple closed-form solution, we can use numerical or approximation methods to find the solution.