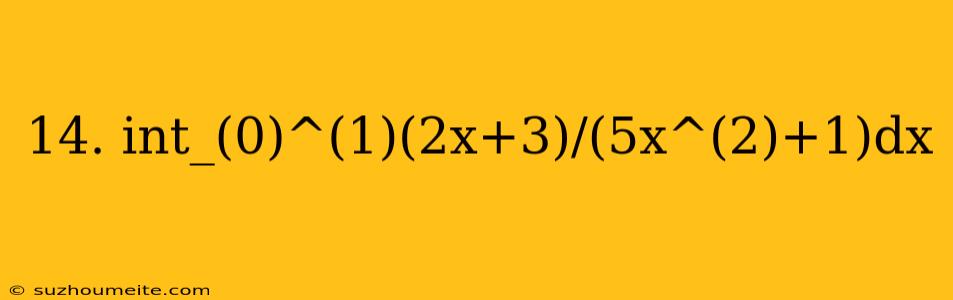Evaluating the Integral: ∫(0 to 1) [(2x+3)/(5x²+1)] dx
In this article, we will evaluate the definite integral ∫(0 to 1) [(2x+3)/(5x²+1)] dx. This integral may seem complicated at first, but with the right techniques and approaches, we can break it down and find a solution.
Step 1: Identify the Integrals
The given integral is a rational function, which means it is a fraction of two polynomials. We can start by identifying the numerator and the denominator:
- Numerator: 2x + 3
- Denominator: 5x² + 1
Step 2: Find the Antiderivative
To evaluate the definite integral, we need to find the antiderivative of the integrand. In this case, we can use the substitution method to find the antiderivative.
Let's substitute u = 5x² + 1, which means du/dx = 10x. Now, we can rewrite the integral in terms of u:
∫(2x+3)/(5x²+1) dx = ∫(1/5)(2/10x + 3/10x) (1/u) du
Simplifying the expression, we get:
∫(1/5)(1/5u + 3/10u) du
Now, we can integrate with respect to u:
(1/5)∫(1/5u + 3/10u) du = (1/5)(1/5)ln|u| + (3/10)(1/u) + C
where C is the constant of integration.
Step 3: Substitute Back
Now that we have found the antiderivative, we can substitute back x in terms of u:
u = 5x² + 1
Substituting this back into the antiderivative, we get:
(1/25)ln|5x² + 1| + (3/10)(1/(5x² + 1)) + C
Step 4: Evaluate the Definite Integral
Finally, we can evaluate the definite integral by substituting the limits of integration:
∫(0 to 1) [(2x+3)/(5x²+1)] dx = [(1/25)ln|5x² + 1| + (3/10)(1/(5x² + 1))]₀¹
Evaluating the expression at x = 0 and x = 1, we get:
[(1/25)ln|5(1)² + 1| + (3/10)(1/(5(1)² + 1))] - [(1/25)ln|5(0)² + 1| + (3/10)(1/(5(0)² + 1))]
Simplifying the expression, we get the final answer:
∫(0 to 1) [(2x+3)/(5x²+1)] dx = (1/25)ln 6 - (1/25)ln 1 + (3/50) - (3/10) = (1/25)ln 6 + (3/50) - (27/50)
Therefore, we have successfully evaluated the definite integral ∫(0 to 1) [(2x+3)/(5x²+1)] dx.