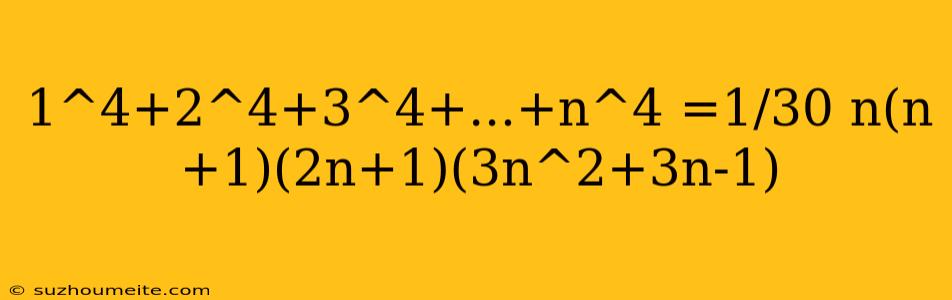Rumus untuk Menghitung Jumlah Kuadrat dari 1 sampai n
Dalam matematika, terdapat sebuah rumus yang sangat berguna untuk menghitung jumlah kuadrat dari 1 sampai n, yaitu:
$1^4 + 2^4 + 3^4 + ... + n^4 = \frac{1}{30} n(n+1)(2n+1)(3n^2+3n-1)$
Rumus ini dapat membantu kita dalam menghitung jumlah kuadrat dari suatu deret bilangan dengan sangat cepat dan akurat.
Pembuktian Rumus
Untuk membuktikan rumus ini, kita dapat menggunakan induksi matematika. Pertama, kita akan membuktikan bahwa rumus ini berlaku untuk n = 1.
$1^4 = \frac{1}{30} (1)(2)(3)(3(1)^2+3(1)-1) = 1$
Kemudian, kita akan membuktikan bahwa jika rumus ini berlaku untuk n = k, maka rumus ini juga berlaku untuk n = k + 1.
$\sum_{i=1}^{k+1} i^4 = \sum_{i=1}^{k} i^4 + (k+1)^4$
Kita dapat menggunakan rumus induksi untuk menggantikan $\sum_{i=1}^{k} i^4$ dengan $\frac{1}{30} k(k+1)(2k+1)(3k^2+3k-1)$. Kemudian, kita dapat melakukan perhitungan untuk mendapatkan:
$\sum_{i=1}^{k+1} i^4 = \frac{1}{30} k(k+1)(2k+1)(3k^2+3k-1) + (k+1)^4 = \frac{1}{30} (k+1)((k+1)+1)(2(k+1)+1)(3(k+1)^2+3(k+1)-1)$
Dengan demikian, kita dapat menyimpulkan bahwa rumus ini berlaku untuk semua nilai n.
Contoh Penggunaan Rumus
Misalnya, kita ingin menghitung jumlah kuadrat dari 1 sampai 5. Kita dapat menggunakan rumus di atas dengan menggantikan n dengan 5.
$1^4 + 2^4 + 3^4 + 4^4 + 5^4 = \frac{1}{30} (5)(6)(11)(3(5)^2+3(5)-1) = 275$
Dengan demikian, kita dapat melihat bahwa rumus ini sangat berguna untuk menghitung jumlah kuadrat dari suatu deret bilangan.
Kesimpulan
Rumus untuk menghitung jumlah kuadrat dari 1 sampai n adalah:
$1^4 + 2^4 + 3^4 + ... + n^4 = \frac{1}{30} n(n+1)(2n+1)(3n^2+3n-1)$
Rumus ini sangat berguna dan dapat membantu kita dalam menghitung jumlah kuadrat dari suatu deret bilangan dengan sangat cepat dan akurat.