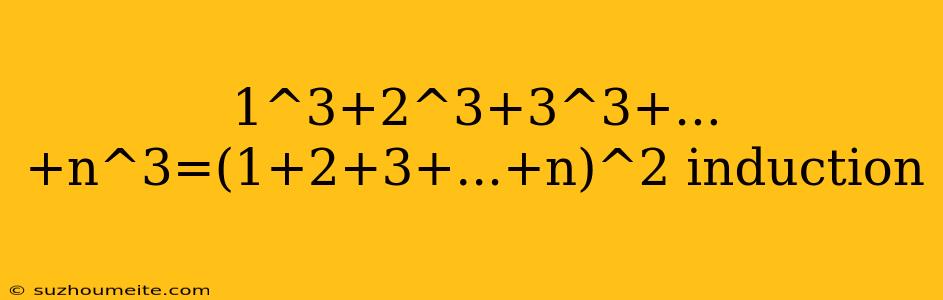Bukti Induksi untuk Rumus 1^3 + 2^3 + 3^3 + … + n^3 = (1 + 2 + 3 + … + n)^2
Rumus di atas membuktikan bahwa jumlah kuadrat dari bilangan prima pertama sampai dengan n, sama dengan kuadrat dari jumlah bilangan prima pertama sampai dengan n. Dalam artikel ini, kita akan membuktikan rumus ini menggunakan metode induksi matematika.
Basis Induksi
Basis induksi memerlukan kita untuk membuktikan bahwa rumus tersebut benar untuk n = 1.
1^3 = 1 = (1)^2
Karena itu, basis induksi terbukti.
Langkah Induksi
Kita mengasumsikan bahwa rumus tersebut benar untuk n = k, sehingga:
1^3 + 2^3 + 3^3 + … + k^3 = (1 + 2 + 3 + … + k)^2
Langkah Induksi untuk n = k + 1
Kita perlu membuktikan bahwa rumus tersebut benar untuk n = k + 1, sehingga:
1^3 + 2^3 + 3^3 + … + k^3 + (k + 1)^3 = (1 + 2 + 3 + … + k + (k + 1))^2
Manipulasi Rumus
Kita dapat memanipulasi rumus di atas menggunakan asumsi kita sebelumnya:
1^3 + 2^3 + 3^3 + … + k^3 + (k + 1)^3 = ((1 + 2 + 3 + … + k)^2 + (k + 1)^3)
=(1 + 2 + 3 + … + k + (k + 1))^2
=(1 + 2 + 3 + … + k)^2 + 2(1 + 2 + 3 + … + k)(k + 1) + (k + 1)^2
Simplifikasi Rumus
Kita dapat menyederhanakan rumus di atas menggunakan beberapa identitas aljabar:
=(1 + 2 + 3 + … + k)^2 + 2(k + 1)(k(k + 1)/2) + (k + 1)^2
=(1 + 2 + 3 + … + k)^2 + (k + 1)^2(k + 1) + (k + 1)^2
=((1 + 2 + 3 + … + k) + (k + 1))^2
=(1 + 2 + 3 + … + k + (k + 1))^2
Kesimpulan
Kita telah membuktikan bahwa rumus 1^3 + 2^3 + 3^3 + … + n^3 = (1 + 2 + 3 + … + n)^2 benar menggunakan metode induksi matematika. Rumus ini membuktikan bahwa jumlah kuadrat dari bilangan prima pertama sampai dengan n, sama dengan kuadrat dari jumlah bilangan prima pertama sampai dengan n.