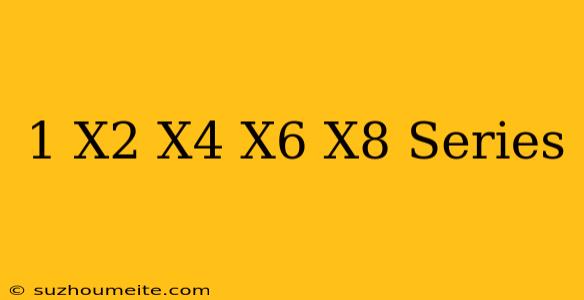The Fascinating World of Alternating Power Sums: 1 - x^2 + x^4 - x^6 + x^8
In the realm of mathematics, there exist certain sequences that have fascinated mathematicians for centuries. One such sequence is the alternating power sum, specifically, the series 1 - x^2 + x^4 - x^6 + x^8. In this article, we will delve into the properties and characteristics of this intriguing sequence.
What is an Alternating Power Sum?
An alternating power sum is a sequence of terms, where each term is a power of a variable (in this case, x) with alternating signs. The sequence can be represented as:
1 - x^2 + x^4 - x^6 + x^8 - ...
The dots at the end indicate that the sequence can be extended indefinitely.
Properties of the Sequence
One of the most interesting properties of this sequence is its convergence. The sequence converges for |x| < 1, meaning that as x approaches 1, the sequence approaches a finite value. This property makes the sequence useful in various mathematical applications.
Another important property is the presence of a closed-form expression for the sequence. The closed-form expression is given by:
1 / (1 + x^2)
This expression can be derived using mathematical induction and the properties of geometric series.
Applications of the Sequence
The 1 - x^2 + x^4 - x^6 + x^8 sequence has numerous applications in mathematics and other fields. Some of the notable applications include:
- Trigonometry: The sequence is related to the Taylor series expansion of the sine and cosine functions.
- Complex Analysis: The sequence appears in the study of complex functions, particularly in the context of residue theory.
- Signal Processing: The sequence is used in signal processing techniques, such as filtering and convolution.
Conclusion
In conclusion, the 1 - x^2 + x^4 - x^6 + x^8 sequence is a fascinating example of an alternating power sum. Its unique properties, such as convergence and a closed-form expression, make it a valuable tool in various mathematical applications. The sequence's connections to trigonometry, complex analysis, and signal processing demonstrate its significance in modern mathematics.