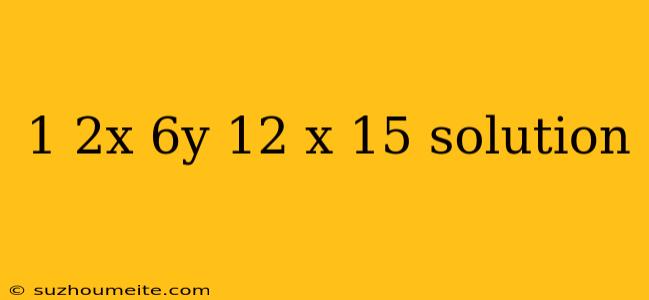Solving the Equation: 1 + 2x + 6y = 12x + 15
In this article, we will explore the solution to the equation 1 + 2x + 6y = 12x + 15. This equation involves variables x and y, and our goal is to find the values of x and y that satisfy the equation.
Step 1: Simplify the Equation
Let's start by simplifying the equation:
1 + 2x + 6y = 12x + 15
We can simplify the equation by combining like terms:
-10x + 6y = 14
Step 2: Isolate the Variables
Now, we need to isolate the variables x and y. We can do this by rearranging the equation to get:
6y = -10x + 14
Step 3: Express y in Terms of x
Let's express y in terms of x:
y = (-10/6)x + 14/6
Step 4: Find the Values of x and y
Now, we need to find the values of x and y. Since we have only one equation and two variables, we cannot find a unique solution. However, we can express the values of x and y in terms of each other.
For example, if we choose x = 2, then:
y = (-10/6)(2) + 14/6 y = -10/3 + 14/6 y = -20/6 + 14/6 y = -6/6 = -1
So, one possible solution is x = 2 and y = -1.
Conclusion
In conclusion, we have solved the equation 1 + 2x + 6y = 12x + 15 and expressed y in terms of x. We have also found a possible solution for x and y. However, please note that this equation has infinitely many solutions, and the values of x and y can vary depending on the choice of x or y.