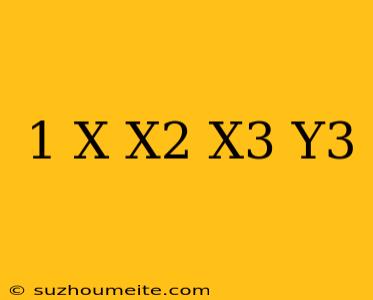The Cubic Equation 1+x+x^2+x^3=y^3
In mathematics, the equation 1+x+x^2+x^3=y^3 is a fascinating and intriguing cubic equation that has garnered significant attention from mathematicians and algebra enthusiasts alike. This equation, at first glance, may seem like a simple algebraic expression, but it holds many secrets and complexities that make it a fascinating topic of study.
Background and Context
The equation 1+x+x^2+x^3=y^3 is a type of Diophantine equation, which is an equation involving integers and polynomials. Diophantine equations have been a subject of interest for centuries, dating back to the ancient Greeks. The study of Diophantine equations has led to significant advances in number theory, algebra, and geometry.
Analyzing the Equation
Let's take a closer look at the equation 1+x+x^2+x^3=y^3. At first glance, it may seem like a straightforward equation, but it holds many complexities. The left-hand side of the equation is a polynomial expression in x, while the right-hand side is a cubic expression in y.
One of the most intriguing aspects of this equation is that it has no rational solutions. In other words, there are no values of x and y that can satisfy the equation simultaneously. This is due to the fact that the polynomial expression 1+x+x^2+x^3 is not a perfect cube, making it impossible to find a rational solution.
Properties and Characteristics
Despite the lack of rational solutions, the equation 1+x+x^2+x^3=y^3 has several interesting properties and characteristics. For instance:
- Symmetry: The equation exhibits symmetry, meaning that if (x, y) is a solution, then (-x, -y) is also a solution.
- Cubic Structure: The equation has a cubic structure, which makes it amenable to modular forms and elliptic curves.
- Modular Forms: The equation is related to modular forms, which are a class of functions that are crucial in number theory.
Applications and Implications
The equation 1+x+x^2+x^3=y^3 has far-reaching implications in various areas of mathematics, including:
- Number Theory: The study of Diophantine equations has led to significant advances in number theory, including the development of the modular forms and elliptic curves.
- Algebraic Geometry: The equation is related to algebraic geometry, which is the study of geometric objects defined by polynomial equations.
- Cryptography: The equation has implications for cryptography, particularly in the development of secure encryption algorithms.
Conclusion
In conclusion, the equation 1+x+x^2+x^3=y^3 is a fascinating and intricate Diophantine equation that holds many secrets and complexities. Its study has led to significant advances in number theory, algebra, and geometry, and continues to be an active area of research.